Отправить мне письмо по E-mail
| 1 | 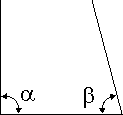 |
Все - курс школьной геометрии. Делаем построение (рисунок). | 2 | 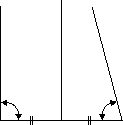 |
Восстанавливаем перпендикуляр из середины нижней стороны. Он является и медианой. | 3 | 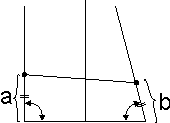 |
Откладываем на сторонах нашего треугольника равные отрезки a и b. Они равны по построению. Соединяем их концы отрезком. |
| 4 | 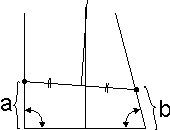 |
Восстанавливаем перпендикуляр из середины получившегося отрезка. | 5 | 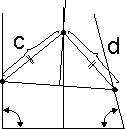 |
Соединяем точку пересечения перпендикуляров с концами равных отрезков, отложенных по сторонам треугольника c и d. | 6 | 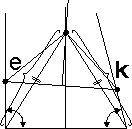 |
Соединяем точку пересечения перпендикуляров с вершинами первоначальных углов e и k. |
| 7 | 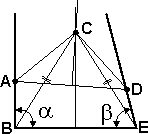 |
Все, с построениями
закончили, теперь само доказательство. Треугольник ABC равен треугольнику CDE по трем сторонам, т.к. AB=DE по построению. AC=CD и BC=CE как стороны двух равнобедренных треугольников (они равнобедренные, т.к. вершина лежит на медиане и высоте). Значит угол ABC=CED (т.к. треугольники их образующие равны). А углы CBE и CEB равны, как углы при основании равнобедренного треугольника. Тогда сумма углов ABC+CBE = CEB+CED. Т.е. прямой угол равен острому! Богу - богово, а кесарю - кесарево! |
||||||
|
|